Introduction:

IH2VOF solves the 2DV Reynolds Averaged Navier–Stokes (RANS) equations at the clear fluid region and the Volume-Averaged Reynolds Averaged Navier–Stokes (VARANS) equations inside the porous media regions, based on the decomposition of the instantaneous velocity and pressure fields into mean and turbulent components, and the κ-ε equations for the turbulent kinetic energy κ, and its dissipation rate ε. This permits the simulation of any kind of coastal structure (e.g. rubble mound, vertical or mixed breakwaters). The free surface movement is tracked by the volume of fluid (VOF) method for one phase only, water and void.

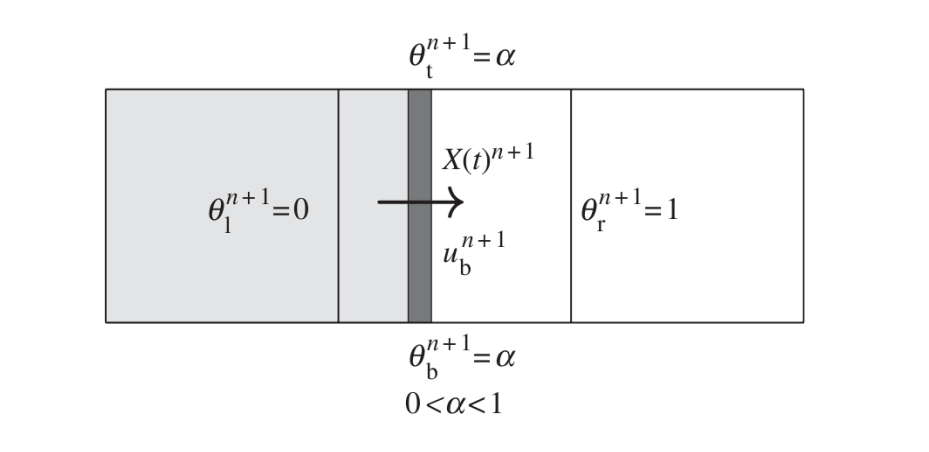
In order to replicate solid bodies immersed in the mesh, instead of treating them as sawtooth-shape, the model uses a cutting cell method first presented by Clarke et al. (1986). The main purpose of this technique is to use an orthogonal structured mesh in the simulations to save computational cost. This approach defines the openness function θ to define the fraction of volume of free space in the cell. According to this definition θ = 0 is a ’solid cell’ (entirely occupied by the solid), θ = 1 is a ’fluid cell’ and 0 < θ < 1 is a ’partial cell’. Variables in the cell or on the cell faces are redefined by the product of the openness coefficients times the original variables. To numerically implement this, partial cell coefficients need to be defined at both the cell centers and boundaries: θl , θr , θt , θb , which correspond to the openness at the left, right, top and bottom, respectively.

IH2VOF includes a complete set of wave generation boundary conditions, which cover the vast majority of the range of relative water depths. These include a Dirichlet boundary condition and a moving boundary method, which are linked with an active wave absorption system to avoid an increase of the mean water level and the agitation. Also an internal source function can be used to generate waves, but it has to be linked with a dissipation zone. For further details see the Dirichlet Boundary Condition.

Governing Equations:

The RANS equations (clear fluid region) are redefined as follows:

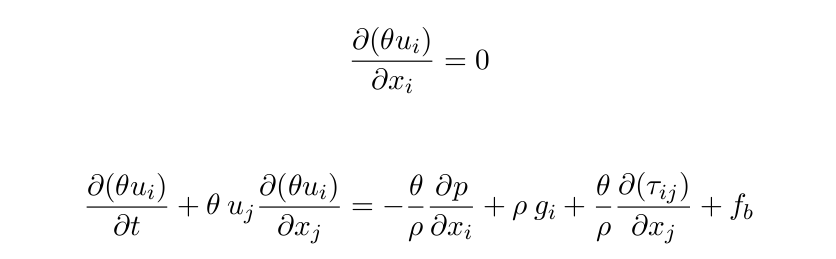
The last term in the second equation is a virtual force. It appears because the IH2VOF model considers two different numerical techniques to simulate moving bodies within the computational domain. The first one is called ’virtual force method’ (see Mittal & Iaccarino 2005) and the other one is the ’direct forcing method’ (Mohd-Yusof 1997). This allows moving boundaries, which can be used to generate and absorb waves as piston wavemakers.

The flow inside the porous media is modeled by solving the VARANS equations, first presented by Hsu et al. (2002). These equations are derived by integrating the RANS equations over a control volume, and their final form is presented below:

The effects of the porous media are controlled by  the porosity (n) and the mean size of the rocks (D50), and 3 friction coefficients (α, β and Ca). These have been thoroughly characterized for all kind of porous structures (berms, core…) and for porous beaches.